专题:
tan15°=2-√3≈0.27。tan15°=tan(60°-45°)=(tan60°- tan45°)/(1+ tan60°*tan45°)=(√3 -1)/(1+√3)=(√3-1)*(√3-1)/[(√3+1)(√3-1)]=(4-2√3)/2=2-√3。

tan15°怎么算
根据三角形外角等于和它不相邻的两个内角和,可延长CB至D,使BD=AB,连接AD.则可根据原△ABC中线段的值求解tan15°的值.
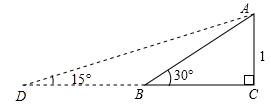
解答:解:延长CB至D,使BD=AB,连接AD.
那么∠D=15°.
∵AB=2,AC=1,∠ABC=30°,
∴BC=√3,
又AB=BD=2,
∴DC=BC+BD=√3+2,
直角三角形ACD中,tan15°=AC/BD=2-√3.
点评:本题综合考查了三角形内角与外角,等腰三角形的性质等知识点.要特别注意辅助线的作法.
tan正切函数图像的性质
定义域:{x|x≠(π/2)+kπ,k∈Z}
值域:R
奇偶性:有,为奇函数
周期性:有
最小正周期:π
单调性:有
单调增区间:(-π/2+kπ,+π/2+kπ),k∈Z
单调减区间:无