专题:
内插法又称插值法。根据未知函数f(x)在某区间内若干点的函数值,作出在该若干点的函数值与f(x)值相等的特定函数来近似原函数f(x),进而可用此特定函数算出该区间内其他各点的原函数f(x)的近似值,这种方法,称为内插法。

内插法原理
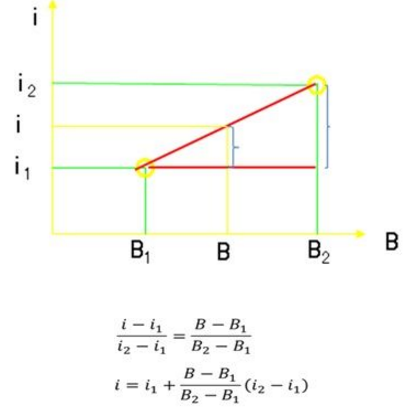
数学内插法即“直线插入法”。其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。A、B、P三点共线,则
(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法公式
求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
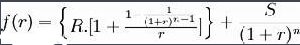
以每期租金先付为例,函数如下:
A表示租赁开始日租赁资产的公平价值; R表示每期租金数额;
S表示租赁资产估计残值;
n表示租期;
r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率
内插法简单计算方法
情形1:B与i同方向变化
情形2:B与i反方向变化

i1<i<i2 B1<B<B2
排列好:
i1B1
i B
i2B2
再相对应相减相除:i→B......
不用再管他谁大谁小,只要i与B对应不要错就可以了。