2022年高考数学考试要仔细审题,清楚题目要求你解决什么问题,然后有条不紊迅速解题,提高准确率。下面是2022年高考数学的评分细则及答题技巧,一起来看!

2022年高考数学评分细则
数学阅卷流程
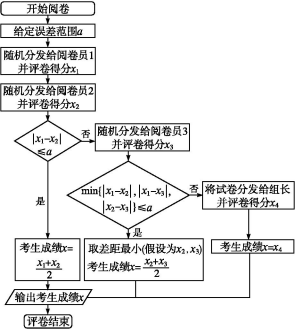
不同题型的评分细则
三角形解答题

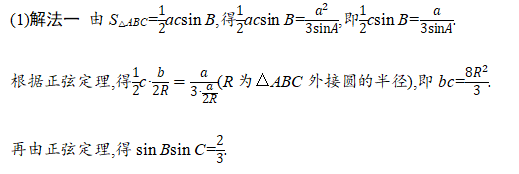


三角函数题目属于高考题中的低中档题,但每年考生的得分情况都不理想,如公式记忆不清、解题方法不明、解题方法选择不当等问题屡屡出现,不能保证作答“会而对,对而全,全而美”。

数列解答题

 概率与统计解答题
概率与统计解答题
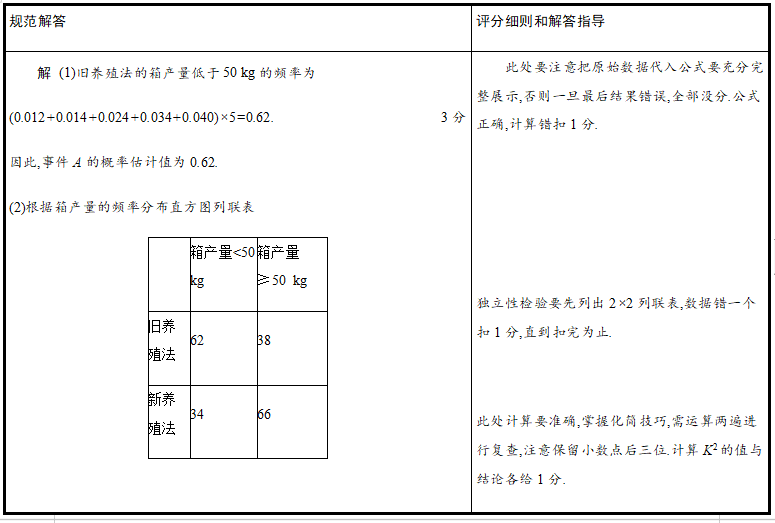



1.正确阅读理解,弄清题意:与概率统计有关的应用问题经常以实际生活为背景,且常考常新,而解决问题的关键是理解题意,弄清本质,将实际问题转化为数学问题求解。
2.对互斥事件要把握住不能同时发生,而对于对立事件除不能同时发生外,其并事件应为必然事件,这些也可类比集合进行理解,具体应用时,可把所有试验结果写出来,看所求事件包含哪几个试验结果,从而断定所给事件的关系。3.用频率分布直方图解决相关问题时,应正确理解图表中各个量的意义,识图掌握信息是解决该类问题的关键。
4.某些数据的变动对中位数可能没有影响。中位数可能出现在所给数据中,也可能不在所给数据中。当一组数据中的个别数据变动较大时,可用中位数描述其集中趋势。平均数与方差都是重要的数字特征,是对总体的一种简明的描述,它们所反映的情况有着重要的实际意义,平均数、中位数、众数描述其集中趋势,方差和标准差描述其波动大小。
5.独立性检验的注意事项
(1)在列联表中注意事件的对应及相关值的确定,不可混淆。K2的观测值k的计算公式很复杂,在解题中易混淆一些数据的意义,代入公式时出错,而导致整个计算结果出错。
(2)对判断结果进行描述时,注意对象的选取要准确无误,应是对假设结论进行的含概率的判断,而非其他。
立体几何解答题



1.证明线面垂直时,不要忽视“面内两条直线为相交直线”这一条件,如第(1)问中,学生易忽视“DO∩BO=O”,导致条件不全而减分;
2.求四面体的体积时,要注意“等体积法”的应用,即合理转化四面体的顶点和底面,目的是底面积和顶点到底面的距离容易求得;
3.注意利用第(1)问的结果:在题设条件下,如果第(1)问的结果第(2)问能用得上,可以直接用,有些题目不用第(1)问的结果甚至无法解决,如本题中,由(1)及题设知∠ADC=90°。
4.要注意书写过程规范,计算结果正确。书写规范是计算正确的前提,在高考这一特定的环境下,学生更要保持规范书写,力争一次成功,但部分学生因平时习惯,解答过程中书写混乱,导致失误过多。
阅卷基本建议
高考数学阅卷对知识点和步骤的把握,公正客观,本着给分有理扣分有据的原则,寻找得分点,否则写再多也是徒劳的。
但是也并非完全无情,比如有少数考生答题错位,会被要求作为异常试卷提交,由专家组特殊处理,而不是直接判了零分等。为此,总结如下解题中需要把握的准则:
1.阅卷速度以秒计,规范答题少丢分
高考阅卷评分标准非常细,按步骤、得分点给分,评阅分步骤、采“点”给分。关键步骤,有则给分,无则没分。所以考场答题应尽量按得分点、步骤规范书写。阅卷中强调关注结果,过程可采用不同的方法阐述。
2.不求巧妙用通法,通性通法要强化
高考评分细则只对主要解题方法,也是最基本的方法,给出详细得分标准,所以用常规方法往往与参考答案一致,比较容易抓住得分点。阅卷中把握见点得分,踩点得分,上下不牵连的原则。
3.干净整洁保得分,简明扼要是关键
若书写整洁,表达清楚,一定会得到合理或偏高的分数,若不规范可能就会吃亏。若写错需改正,只需划去,不要乱涂乱划,否则易丢分。
4.狠抓基础保成绩,分步解决克难题
(1)基础题争取得满分。
涉及的定理、公式要准确,数学语言要规范,仔细计算,争取前3个解答题及选考不丢分。
(2)压轴题争取多得分。
第(1)问一般难度不大,要保证得分,第(2)问若不会,也要根据条件或第(1)问的结论推出一些结论,可能就是得分点。
高考数学的答题技巧
解题格式要规范,重点步骤要突出。
选择题时间控制在35分中以内。小题小做、巧做、简单做,选择题和填空题要多用数形结合、特殊值验证法等技巧,节约时间。
保持心静,以不变应万变。切莫因旁人的翻卷或其他行为干扰自己的解决思路。这些都是高考数学应试答题高分技巧。

