专题:
高中数学中,我们会遇到很多公式定理,这些公式定理是解答问题的基础。本期小编整理了椭圆的面积公式,以及椭圆的标准方程,看看这些公式是如何推导出来的吧,并附上椭圆的定义,大家也可以关注黑边网站,里面有很多学习干货。

一、椭圆的定义
我们把平面内到两定点的距离和等于常数(大于这两个定点的间距离)的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距,焦距的一半称为半焦距。
二、椭圆的面积公式
椭圆的面试公式是S=πab。
习惯上,把椭圆的长轴长度记为“2a”,并把以椭圆的对称中心为端点的长轴的一半称作这个椭圆的长半轴;把椭圆的短轴长度记为“2b”,并把以椭圆的对称中心为端点的短轴的一半称作这个椭圆的短半轴。
有了“长半轴”和“短半轴”的概念后,任何一个椭圆的面积公式就可以表述为:“椭圆的面积等于圆周率π与长半轴长、短半轴长这三者间的乘积”,用数学公式可以表示为:S=πab。
三、椭圆的标准方程
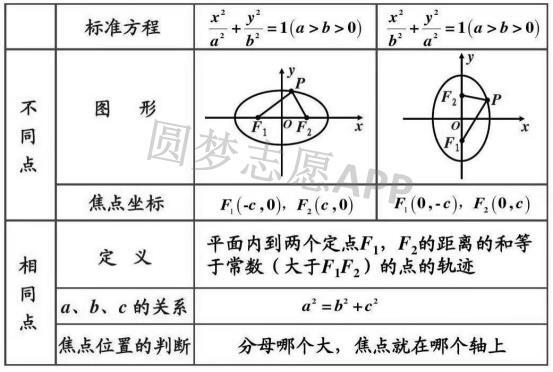
我们把对称中心在平面直角坐标系的原点,并且两焦点在同一条坐标轴上的椭圆的方程称为椭圆的标准方程。椭圆的标准方程有“焦点在x轴”和“焦点在y轴”两种形式。
1、焦点在x轴:x^2/a^2+y^2/b^2=1(a>b>0)
2、焦点在y轴:y^2/a^2+x^2/b^2=1(a>b>0)
其中a^2-c^2=b^2。
更多内容大家可以点击本文下方输入分数,一键进入大文学,了解查看。