关于高中数学中,点到平面的距离公式怎么计算是大家平时问的最多的一个问题,点到平面距离是指空间内一点到平面内一点的最小长度。点到平面的距离公式:d=|Ax0+By0+Cz0+D|/√(A²+B²+C²)。黑边网小编还将为大家带来空间中点到平面的距离公式怎么求的解答。
一、点到平面的距离公式
1、 平面中点到直线的距离
平面上点P(x0,y0)到直线Ax+By+C=0的距离d的公式为:
d=|Ax0+By0+Cz0+D|/√(A²+B²+C²)。
用向量法计算点到平面的距离,就是把点和平面放在直角坐标系下进行计算。这样,点和平面均可用坐标来表示:

2、空间中平面的方程
设空间中平面α的法向量为(A,B,C),且过点P(x0,y0,z0),则该平面的方程为:
A(x-x0)+B(y-y0)+C(z-z0)=0
由于该方程利用平面上一点以及平面的法向量,所以被称为平面的点法式方程。
将上述方程展开,则得到平面的一般式方程:Ax+By+Cz+D+0,其中,D=Ax0+By0+Cz0。
二、空间中点到平面的距离公式怎么求?
类似平面中点到直线的距离公式,若空间中点到平面的距离为d,则空间中点到平面的距离公式为:
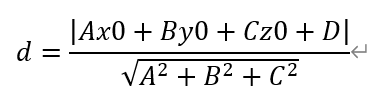
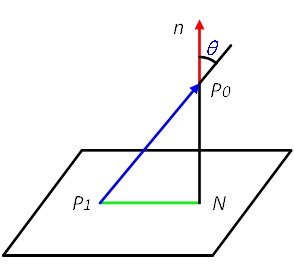
三、平面的相关知识点
为了帮助大家更好的学习掌握点到平面距离公式的相关知识,黑边网小编为大家介绍3个平面的相关知识点,包括平面的一般式方程、向量的模(长度)、向量的点积(内积)
平面的一般式方程
Ax +By +Cz + D = 0
其中n = (A, B, C)是平面的法向量,D是将平面平移到坐标原点所需距离(所以D=0时,平面过原点)
向量的模(长度)
给定一个向量V(x, y, z),则|V| = sqrt(x * x + y * y + z * z)
向量的点积(内积)
给定两个向量V1(x1, y1, z1)和V2(x2, y2, z2)则他们的内积是
V1V2 = x1x2 + y1y2 + z1z2
大家从本文下方“输入分数看能上的大学”一栏,输入成绩、地区、选考科目,一键进入大文学,查看更多大学投档线线、专业分数线及位次、大学排名等数据。
同时大文学还可以通过大数据分析及云计算处理,为我们科学评估所有能上的大学以及被录取的概率,方便我们后续志愿填报选择学校参考!