高高中的函数是高考的重点内容,函数知识也比较难。那么三次函数的对称中心要怎么看呢?新高三小编整理了以下三次函数对称中心的证明,欢迎参考。

三次函数有对称中心的证明
证明:
因为f(x)=a(x-x0)3+b(x-x0)+y0的对称中心是(x0,y0),即(x0,f(x0))
所以f(x)=ax3+bx2+cx+d如果能写成f(x)=a(x-x0)3+b(x-x0)+y0那么三次函数的对称中心就是(x0,f(x0))
所以设f(x)=a(x+m)3+p(x+m)+n
得f(x)=ax3+3amx2+(3am2+p)x+am3+pm+n
所以3am=b; 3am2+p=c; am3+pm+n=d;
所以m=b/3a; p=(3ac-b2)/3a; n=d+(2b3)/(27a2)-bc/(3a)
所以f(x)=a(x+b/3a)3+(c-B2/3a)(x+b/3a)+d+2b3/27a2-bc/3a
得证。
三次函数对称中心证明推广
如果f(x)是一个n次多项式,n>=2(因为直线的对称中心从狭义上讲是没有对称中心 而在广义上讲是无数个对称中心),其n次项系数是a0,n-1次项系数是a1,则有
⑴:如果y=f(x)的图像是中心对称图形,其对称中心是(-a1/n/a0,f(-a1/n/a0));
⑵:如果y=f(x)的图像是轴对称图形,其对称轴是x=-a1/n/a0.
小编推荐:指数函数的单调性如何证明
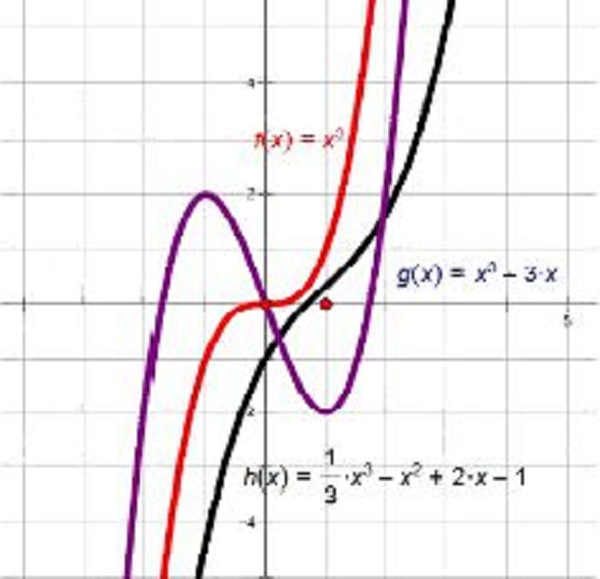
三次函数的图像一定中心对称吗
三次函数的图像一定是中心对称图形,其对称中心是(-a1/n/a0,f(-a1/n/a0));
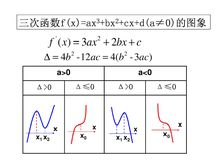
最高次数项为3的函数,形如y=ax³+bx²+cx+d(a≠0,b,c,d为常数)的函数叫做三次函数(cubics function)。 三次函数的图象是一条曲线——回归式抛物线(不同于普通抛物线)。
三次函数性态的五个要点:
⒈三次函数y=f(x)在(-∞,+∞)上的极值点的个数
⒉三次函数y=f(x)的图象与x 轴交点个数
⒊单调性问题
⒋三次函数f(x)图象的切线条数
⒌融合三次函数和不等式,创设情境求参数的范围