参考公式:柱体的体积 ,其中
,其中 是柱体的底面积,
是柱体的底面积, 是柱体的高.
是柱体的高.
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.已知集合 ,则
,则 .
.
2.已知 是虚数单位,则复数
是虚数单位,则复数 的实部是 .
的实部是 .
3.已知一组数据 的平均数为4,则
的平均数为4,则 的值是 .
的值是 .
4.将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是 .
5.如图是一个算法流程图,若输出 的值为
的值为 ,则输入
,则输入 的值是 .
的值是 .

6.在平面直角坐标系xOy中,若双曲线 的一条渐近线方程为
的一条渐近线方程为 ,则该双曲线的离心率是 .
,则该双曲线的离心率是 .
7.已知y=f(x)是奇函数,当x≥0时, ,则
,则 的值是 .
的值是 .
8.已知 =
= ,则
,则 的值是 .
的值是 .
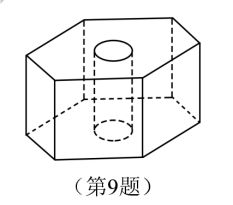
9.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半轻为0.5 cm,则此六角螺帽毛坯的体积是 cm.
10.将函数 的图象向右平移
的图象向右平移 个单位长度,则平移后的图象中与y轴最近的对称轴的方程是 .
个单位长度,则平移后的图象中与y轴最近的对称轴的方程是 .
11.设{an}是公差为d的等差数列,{bn}是公比为q的等比数列.已知数列{an+bn}的前n项和 ,则d+q的值是 .
,则d+q的值是 .
12.已知 ,则
,则 的最小值是 .
的最小值是 .
13.在△ABC中, D在边BC上,延长AD到P,使得AP=9,若
D在边BC上,延长AD到P,使得AP=9,若 (m为常数),则CD的长度是 .
(m为常数),则CD的长度是 .

14.在平面直角坐标系xOy中,已知 ,A,B是圆C:
,A,B是圆C: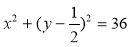 上的两个动点,满足
上的两个动点,满足 ,则△PAB面积的最大值是 .
,则△PAB面积的最大值是 .
二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(14分)在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.
(1)求证:EF∥平面AB1C1;(2)求证:平面AB1C⊥平面ABB1.

16.(14分)
在△ABC中,角A,B,C的对边分别为a,b,c,已知 .
.
(1)求 的值;
的值;
(2)在边BC上取一点D,使得 ,求
,求 的值.
的值.

17.(14分)
某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O在水平线MN上,桥AB与MN平行, 为铅垂线(
为铅垂线( 在AB上).经测量,左侧曲线AO上任一点D到MN的距离
在AB上).经测量,左侧曲线AO上任一点D到MN的距离 (米)与D到
(米)与D到 的距离a(米)之间满足关系式
的距离a(米)之间满足关系式 ;右侧曲线BO上任一点F到MN的距离
;右侧曲线BO上任一点F到MN的距离 (米)与F到
(米)与F到 的距离b(米)之间满足关系式
的距离b(米)之间满足关系式 .已知点B到
.已知点B到 的距离为40米.
的距离为40米.
(1)求桥AB的长度;
(2)计划在谷底两侧建造平行于 的桥墩CD和EF,且CE为80米,其中C,E在AB上(不包括端点)..桥墩EF每米造价k(万元)、桥墩CD每米造价
的桥墩CD和EF,且CE为80米,其中C,E在AB上(不包括端点)..桥墩EF每米造价k(万元)、桥墩CD每米造价 (万元)(k>0),问
(万元)(k>0),问 为多少米时,桥墩CD与EF的总造价最低?
为多少米时,桥墩CD与EF的总造价最低?

18.(16分)
在平面直角坐标系xOy中,已知椭圆 的左、右焦点分别为F1,F2,点A在椭圆E上且在第一象限内,AF2⊥F1F2,直线AF1与椭圆E相交于另一点B.
的左、右焦点分别为F1,F2,点A在椭圆E上且在第一象限内,AF2⊥F1F2,直线AF1与椭圆E相交于另一点B.

(1)求 的周长;
的周长;
(2)在x轴上任取一点P,直线AP与椭圆E的右准线相交于点Q,求 的最小值;
的最小值;
(3)设点M在椭圆E上,记 与
与 的面积分别为S1,S2,若
的面积分别为S1,S2,若 ,求点M的坐标.
,求点M的坐标.
19.(16分)
已知关于x的函数 与
与 在区间D上恒有
在区间D上恒有 .
.
(1)若 ,求h(x)的表达式;
,求h(x)的表达式;
(2)若 ,求k的取值范围;
,求k的取值范围;
(3)若
 求证:
求证: .
.
20.(16分)已知数列 的首项a1=1,前n项和为Sn.设λ与k是常数,若对一切正整数n,均有
的首项a1=1,前n项和为Sn.设λ与k是常数,若对一切正整数n,均有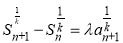 成立,则称此数列为“λ~k”数列.
成立,则称此数列为“λ~k”数列.
(1)若等差数列 是“λ~1”数列,求λ的值;
是“λ~1”数列,求λ的值;
(2)若数列 是“
是“ ”数列,且
”数列,且 ,求数列
,求数列 的通项公式;
的通项公式;
(3)对于给定的λ,是否存在三个不同的数列 为“λ~3”数列,且
为“λ~3”数列,且 ?若存在,求λ的取值范围;若不存在,说明理由.
?若存在,求λ的取值范围;若不存在,说明理由.
 2023年江苏省高考仿真数学试卷答案
2023年江苏省高考仿真数学试卷答案
1. 2.3 3.2 4.
2.3 3.2 4. 5.
5. 6.
6. 7.
7. 8.
8. 9.
9.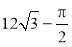 10.
10. 11.4 12.
11.4 12. 13.
13. 或0 14.
或0 14.
15.证明:因为 分别是
分别是 的中点,所以
的中点,所以 .
.
又 平面
平面 ,
,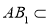 平面
平面 ,
,
所以 平面
平面 .
.

(2)因为 平面
平面 ,
, 平面
平面 ,
,
所以 .
.
又 ,
, 平面
平面 ,
,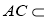 平面
平面 ,
,
所以 平面
平面 .
.
又因为 平面
平面 ,所以平面
,所以平面 平面
平面 .
.
16.解:(1)在 中,因为
中,因为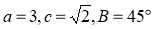 ,
,
由余弦定理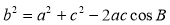 ,得
,得 ,
,
所以 .
.
在 中,由正弦定理
中,由正弦定理 ,
,
得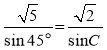 ,
,
所以
(2)在 中,因为
中,因为 ,所以
,所以 为钝角,
为钝角,
而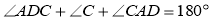 ,所以
,所以 为锐角.
为锐角.
故 则
则 .
.
因为 ,所以
,所以 ,
, .
.
从而
 .
.
17.解:(1)设 都与
都与 垂直,
垂直, 是相应垂足.
是相应垂足.
由条件知,当 时,
时,
 则
则 .
.
由 得
得
所以 (米).
(米).

(2)以 为原点,
为原点, 为
为 轴建立平面直角坐标系
轴建立平面直角坐标系 (如图所示).
(如图所示).
设 则
则
 .
.
因为 所以
所以 .
.
设 则
则
所以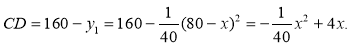
记桥墩 和
和 的总造价为
的总造价为 ,
,
则
 ,
,
令 得
得

所以当 时,
时, 取得最小值.
取得最小值.
答:(1)桥 的长度为120米;
的长度为120米;
(2)当 为20米时,桥墩
为20米时,桥墩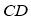 和
和 的总造价最低.
的总造价最低.
18.解:(1)椭圆 的长轴长为
的长轴长为 ,短轴长为
,短轴长为 ,焦距为
,焦距为 ,
,
则 .
.
所以 的周长为
的周长为 .
.
(2)椭圆 的右准线为
的右准线为 .
.
设 ,
,
则 ,
,

在 时取等号.
时取等号.
所以 的最小值为
的最小值为 .
.

(3)因为椭圆 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 在椭圆
在椭圆 上且在第一象限内,
上且在第一象限内, ,
,
则 .
.
所以直线
设 ,因为
,因为 ,所以点
,所以点 到直线
到直线 距离等于点
距离等于点 到直线
到直线 距离的3倍.
距离的3倍.
由此得 ,
,
则 或
或 .
.
由 得
得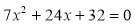 ,此方程无解;
,此方程无解;
由 得
得 ,所以
,所以 或
或 .
.
代入直线 ,对应分别得
,对应分别得 或
或 .
.
因此点 的坐标为
的坐标为 或
或 .
.
19.解:(1)由条件 ,得
,得 ,
,
取 ,得
,得 ,所以
,所以 .
.
由 ,得
,得 ,此式对一切
,此式对一切 恒成立,
恒成立,
所以 ,则
,则 ,此时
,此时 恒成立,
恒成立,
所以 .
.
(2) .
.
令 ,则
,则 令
令 ,得
,得 .
.

所以 .则
.则 恒成立,
恒成立,
所以当且仅当 时,
时, 恒成立.
恒成立.
另一方面, 恒成立,即
恒成立,即 恒成立,
恒成立,
也即 恒成立.
恒成立.
因为 ,对称轴为
,对称轴为 ,
,
所以 ,解得
,解得 .
.
因此,k的取值范围是
(3)①当 时,
时,
由 ,得
,得 ,整理得
,整理得

令 则
则 .
.
记
则 恒成立,
恒成立,
所以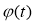 在
在 上是减函数,则
上是减函数,则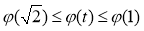 ,即
,即 .
.
所以不等式 有解,设解为
有解,设解为 ,
,
因此 .
.
②当 时,
时,
 .
.
设 ,
,
令 ,得
,得 .
.
当 时,
时, ,
, 是减函数;
是减函数;
当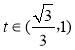 时,
时, ,
, 是增函数.
是增函数.
 ,
, ,则当
,则当 时,
时, .
.
(或证: .)
.)
则 ,因此
,因此 .
.
因为 ,所以
,所以 .
.
③当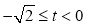 时,因为
时,因为 ,
, 均为偶函数,因此
均为偶函数,因此 也成立.
也成立.
综上所述, .
.
20.解:(1)因为等差数列 是“λ~1”数列,则
是“λ~1”数列,则 ,即
,即 ,
,
也即 ,此式对一切正整数n均成立.
,此式对一切正整数n均成立.
若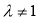 ,则
,则 恒成立,故
恒成立,故 ,而
,而 ,
,
这与 是等差数列矛盾.
是等差数列矛盾.
所以 .(此时,任意首项为1的等差数列都是“1~1”数列)
.(此时,任意首项为1的等差数列都是“1~1”数列)
(2)因为数列 是“
是“ ”数列,
”数列,
所以 ,即
,即 .
.
因为 ,所以
,所以 ,则
,则 .
.
令 ,则
,则 ,即
,即 .
.
解得 ,即
,即 ,也即
,也即 ,
,
所以数列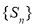 是公比为4的等比数列.
是公比为4的等比数列.
因为 ,所以
,所以 .则
.则
(3)设各项非负的数列 为“
为“ ”数列,
”数列,
则 ,即
,即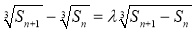 .
.
因为 ,而
,而 ,所以
,所以 ,则
,则 .
.
令 ,则
,则 ,即
,即 .(*)
.(*)
①若 或
或 ,则(*)只有一解为
,则(*)只有一解为 ,即符合条件的数列
,即符合条件的数列 只有一个.
只有一个.
(此数列为1,0,0,0,…)
②若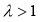 ,则(*)化为
,则(*)化为 ,
,
因为 ,所以
,所以 ,则(*)只有一解为
,则(*)只有一解为 ,
,
即符合条件的数列 只有一个.(此数列为1,0,0,0,…)
只有一个.(此数列为1,0,0,0,…)
③若 ,则
,则 的两根分别在(0,1)与(1,+∞)内,
的两根分别在(0,1)与(1,+∞)内,
则方程(*)有两个大于或等于1的解:其中一个为1,另一个大于1(记此解为t).
所以 或
或 .
.
由于数列 从任何一项求其后一项均有两种不同结果,所以这样的数列
从任何一项求其后一项均有两种不同结果,所以这样的数列 有无数多个,则对应的
有无数多个,则对应的 有无数多个.
有无数多个.
综上所述,能存在三个各项非负的数列 为“
为“ ”数列,
”数列, 的取值范围是
的取值范围是 .
.
21.【选做题】本题包括A、B、C三小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
A.[选修4-2:矩阵与变换](10分)
平面上点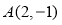 在矩阵
在矩阵 对应的变换作用下得到点
对应的变换作用下得到点 .
.
(1)求实数 ,
, 的值;
的值;
(2)求矩阵 的逆矩阵
的逆矩阵 .
.
B.[选修4-4:坐标系与参数方程](10分)
在极坐标系中,已知点 在直线
在直线 上,点
上,点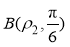 在圆
在圆 上(其中
上(其中 ,
, ).
).
(1)求 ,
, 的值;
的值;
(2)求出直线 与圆
与圆 的公共点的极坐标.
的公共点的极坐标.
C.[选修4-5:不等式选讲](10分)
设 ,解不等式
,解不等式 .
.
【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
22.(10分)
在三棱锥A—BCD中,已知CB=CD= ,BD=2,O为BD的中点,AO⊥平面BCD,AO=2,E为AC的中点.
,BD=2,O为BD的中点,AO⊥平面BCD,AO=2,E为AC的中点.

(1)求直线AB与DE所成角的余弦值;
(2)若点F在BC上,满足BF= BC,设二面角F—DE—C的大小为θ,求sinθ的值.
BC,设二面角F—DE—C的大小为θ,求sinθ的值.
23.(10分)
甲口袋中装有2个黑球和1个白球,乙口袋中装有3个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋,重复n次这样的操作,记甲口袋中黑球个数为Xn,恰有2个黑球的概率为pn,恰有1个黑球的概率为qn.
(1)求p1,q1和p2,q2;
(2)求2pn+qn与2pn-1+qn-1的递推关系式和Xn的数学期望E(Xn)(用n表示) .
数学Ⅱ(附加题)参考答案
21.【选做题】
A.[选修4-2:矩阵与变换]
本小题主要考查矩阵的运算、逆矩阵等基础知识,考查运算求解能力.满分10分.
解:(1)因为 ,所以
,所以
解得 ,所以
,所以 .
.
(2)因为 ,
, ,所以
,所以 可逆,
可逆,
从而 .
.
B.[选修4-4:坐标系与参数方程]
本小题主要考查曲线的极坐标方程等基础知识,考查运算求解能力.满分10分.
解:(1)由 ,得
,得 ;
; ,又(0,0)(即(0,
,又(0,0)(即(0, ))也在圆C上,
))也在圆C上,
因此 或0.
或0.
(2)由 得
得 ,所以
,所以 .
.
因为 ,
, ,所以
,所以 ,
, .
.
所以公共点的极坐标为 .
.
C.[选修4-5:不等式选讲]
本小题主要考查解不等式等基础知识,考查运算求解和推理论证能力.满分10分.
解:当x>0时,原不等式可化为 ,解得
,解得 ;
;
当 时,原不等式可化为
时,原不等式可化为 ,解得
,解得 ;
;
当 时,原不等式可化为
时,原不等式可化为 ,解得
,解得 .
.
综上,原不等式的解集为 .
.
22.【必做题】本小题主要考查空间向量、异面直线所成角和二面角等基础知识,考查空间想象能力和运算求解能力.满分10分.
解:(1)连结OC,因为CB =CD,O为BD中点,所以CO⊥BD.
又AO⊥平面BCD,所以AO⊥OB,AO⊥OC.
以 为基底,建立空间直角坐标系O–xyz.
为基底,建立空间直角坐标系O–xyz.
因为BD=2, ,AO=2,
,AO=2,
所以B(1,0,0),D(–1,0,0),C(0,2,0),A(0,0,2).
因为E为AC的中点,所以E(0,1,1).
则 =(1,0,–2),
=(1,0,–2), =(1,1,1),
=(1,1,1),
所以 .
.
因此,直线AB与DE所成角的余弦值为 .
.
(2)因为点F在BC上, ,
, =(–1,2,0).
=(–1,2,0).
所以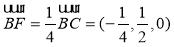 .
.
又 ,
,
故 .
.
设 为平面DEF的一个法向量,
为平面DEF的一个法向量,
则 即
即
取 ,得
,得 ,
, ,所以
,所以 .
.
设 为平面DEC的一个法向量,又
为平面DEC的一个法向量,又 =(1,2,0),
=(1,2,0),
则 即
即 取
取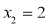 ,得
,得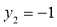 ,
, ,
,
所以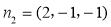 .
.
故 .
.
所以 .
.

23.【必做题】本小题主要考查随机变量及其概率分布等基础知识,考查逻辑思维能力和推理论证能力.满分10分.
解:(1) ,
,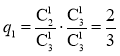 ,
,
 ,
,

 .
.
(2)当 时,
时,
 ,①
,①

 ,②
,②
 ,得
,得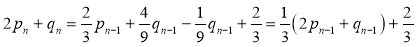 .
.
从而 ,又
,又 ,
,
所以 ,
, .③
.③
由②,有 ,又
,又 ,
,
所以 ,
, .
.
由③,有 ,
, .
.
故 ,
, .
.
 的概率分布
的概率分布
| 0 | 1 | 2 |
|
|
|
|
则 .
.
 2023年
2023年


