- 已知集合,那么
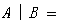 __________.
__________. - 若复数
 满足
满足 ,其中
,其中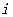 是虚数单位,则
是虚数单位,则 的实部为___________.
的实部为___________. - 已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为________.
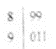
4.一个算法的伪代码如图所示,执行此算法,最后输出的 的值为__________.
的值为__________.

5.函数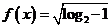 的定义域为__________.
的定义域为__________.
6.某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率是__________.
7.已知函数 的图像关于直线
的图像关于直线 对称,则
对称,则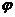 的值是______.
的值是______.
8.在平面直角坐标系 中,若双曲线
中,若双曲线 的右焦点
的右焦点 到一条渐近线的距离为
到一条渐近线的距离为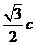 ,则其离心率的值是________
,则其离心率的值是________
9.函数 满足
满足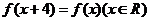 ,且在区间
,且在区间 上
上 ,则
,则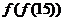 的值为________
的值为________
10.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为______

11.若函数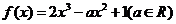 在
在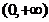 内有且只有一个零点,则
内有且只有一个零点,则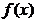 在
在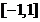 上的最大值与最小值的和为____
上的最大值与最小值的和为____
12.在平面直角坐标系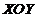 中,
中,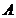 为直线
为直线 上在第一象限内的点,
上在第一象限内的点,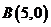 以
以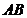 为直径的圆
为直径的圆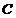 与直线
与直线 交于另一点
交于另一点 ,若
,若 ,则点
,则点 的横坐标为_____
的横坐标为_____
13.在 中,角
中,角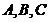 所对应的边分别为
所对应的边分别为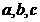
 ,
,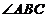 的平分线交
的平分线交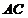 于点
于点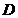 ,且
,且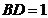 ,则
,则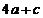 的最小值为__________
的最小值为__________
14.已知集合 ,将
,将 的所有元素从小到大依次排列构成一个数列
的所有元素从小到大依次排列构成一个数列 ,记
,记 为数列的前
为数列的前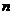 项和,则使得
项和,则使得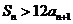 成立的
成立的 的最小值为______.
的最小值为______.
15.在平行四边形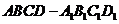 中,
中,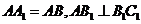
求证:(1)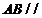 平面
平面
(2)平面 平面
平面

16.已知 为锐角,
为锐角, ,
, 。
。
(1)求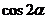 的值。
的值。
(2)求 的值。
的值。
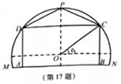
17.某农场有一块农田,如图所示,它的边界由圆 的一段圆弧
的一段圆弧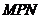 (
(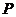 为此圆弧的中点)
为此圆弧的中点)
和线段 构成,已知圆
构成,已知圆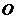 的半径为40米,点
的半径为40米,点 到
到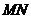 的距离为50米,先规划在此农田
的距离为50米,先规划在此农田
上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形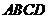 .大棚Ⅱ内的地块形状为
.大棚Ⅱ内的地块形状为
要求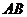 均在线段
均在线段 上,
上, 均在圆弧上,设
均在圆弧上,设 与
与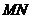 所成的角为
所成的角为
(1)用 分别表示矩形
分别表示矩形 和
和 的面积,并确定
的面积,并确定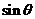 的取值范围
的取值范围
(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年
产值之比为4:3.求当 为何值时,能使甲、乙两种蔬菜的年总产值最大.
为何值时,能使甲、乙两种蔬菜的年总产值最大.
18.如图,在平面直角坐标系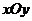 中,椭圆C过点
中,椭圆C过点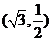 ,焦点
,焦点 ,圆O的直径为
,圆O的直径为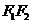 .
.
(1)求椭圆C及圆O的方程;
(2)设直线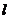 与圆O相切于第一象限内的点P.
与圆O相切于第一象限内的点P.
①若直线 与椭圆C有且只有一个公共点,求点P的坐标;
与椭圆C有且只有一个公共点,求点P的坐标;
②直线 与椭圆C交于A、B两点.若
与椭圆C交于A、B两点.若 的面积为
的面积为 ,求直线
,求直线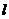 的方程.
的方程.

19.记 分别为函数
分别为函数 的导函数.若存在
的导函数.若存在 ,满足
,满足 且
且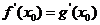 ,则称
,则称 为函数
为函数 与
与 的一个”S点”.
的一个”S点”.
(1)证明:函数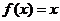 与
与 不存在”S点”.
不存在”S点”.
(2)若函数 与
与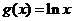 存在”S点”,求实数
存在”S点”,求实数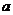 的值.
的值.
(3)已知函数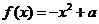 ,
, ,对任意
,对任意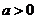 ,判断是否存在
,判断是否存在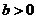 ,使函数
,使函数 与
与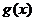 在区间
在区间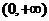 内存在”S点”,并说明理由.
内存在”S点”,并说明理由.
20设{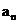 }是首项为
}是首项为 ,公差为
,公差为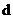 的等差数列,
的等差数列, 是首项
是首项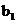 ,公比为q的等比数列
,公比为q的等比数列
(1) 设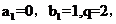 若
若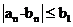 对n=1,2,3,4均成立,求d的取值范围
对n=1,2,3,4均成立,求d的取值范围
(2) 若 ,
, ,
, 证明:存在
证明:存在 ,使得
,使得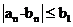 对
对
n=2.3L, 均成立,并求
均成立,并求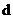 的取值范围(用
的取值范围(用
 表示)。
表示)。