









2019年普通高等学校招生全国统一考试(浙江卷)
数学
选择题部分(共40分)
一、选择题:本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集U={-1,0,1,2,3},集合A={0,1,2},B={-1,0,1},则()∩B=
A.{-1}
B.{0,1}
C.{-1,2,3}
D.{-1,0,1,3}
2.渐进线方程为x±y=0的双曲线的离心率是
A.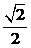
B.1
C.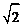
D.2
3.若实数x,y满足约束条件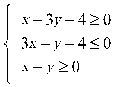 则z=3x+2y的最大值是
则z=3x+2y的最大值是
A.-1
B.1
C.10
D.12
4. 组暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式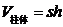 ,其中
,其中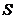 是柱体的底面积,
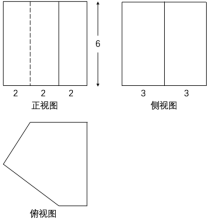
是柱体的底面积,  是柱体的高,若某柱体的三视图如图所示,则该柱体的体积是( )
是柱体的高,若某柱体的三视图如图所示,则该柱体的体积是( )
A. 158
B. 162
C. 182
D. 32

A. 充分不必要条件
B. 必要不充分条件
C. 充分必要条件
D. 既不充分也不必要条件
6.在同一直角坐标系中,函数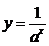 ,
,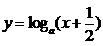 ,(>0且≠0)的图像可能是( )
,(>0且≠0)的图像可能是( )
A.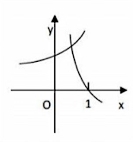
B. 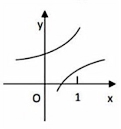
C. 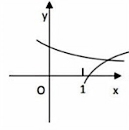
D. 
7.设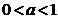 ,随机变量
,随机变量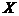 的分布列是( )
的分布列是( )

则当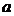 在(0,1)内增大时
在(0,1)内增大时
A. 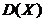 增大
增大
B. 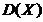 减小
减小
C. 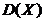 先增大后减小
先增大后减小
D. 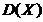 先减小后增大
先减小后增大

9.已知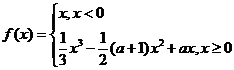 ,函数
,函数 恰有三个零点
恰有三个零点
则( )
A. 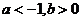
B. 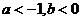
C. 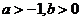
D. 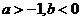
10.设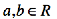 ,数列
,数列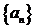 满足
满足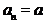 ,
, ,
,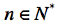 ,则
,则
A.当 时,
时, 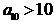
B.当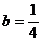 时,
时, 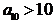
C.当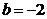 时,
时, 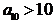
D.当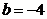 时,
时, 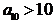
非选择题部分(共110分)
二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
11.复数z = 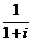 (i为虚数单位),则|
(i为虚数单位),则|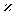 |=
|=
12.已知圆C的圆心坐标是(0,m),半径长是r.若直线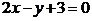 与圆相切与点A(-2,-1),则m= ,r=
与圆相切与点A(-2,-1),则m= ,r=
13.在二项式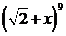 的展开式中,常数项是 ,系数为有理数的项的个数是
的展开式中,常数项是 ,系数为有理数的项的个数是
14.在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,若∠BDC=45°则BD= ,cos∠ABD=
15.已知椭圆 的左焦点为F,点P在椭圆上且在x轴的上方,若线段PF的中点在以原点O为圆心,|OF|为半径的圆上,则直线PF的斜率是
的左焦点为F,点P在椭圆上且在x轴的上方,若线段PF的中点在以原点O为圆心,|OF|为半径的圆上,则直线PF的斜率是
ABC-A柱子﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX﷽﷽﷽﷽﷽XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX16.已知 ,函数
,函数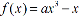 ,若存在
,若存在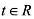 ,使得
,使得 ,则实数
,则实数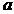 的最大值是
的最大值是

三、解答题:本大题共5小题,共74分。解答应写出文字说明、证明过程或演算步骤。
18.设函数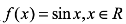
(1)已知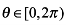 ,函数
,函数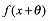 是偶函数,求
是偶函数,求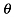 的值.
的值.
(2)求函数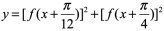 的值域
的值域
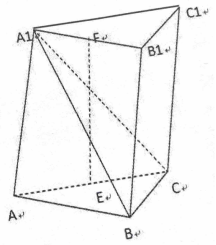
19.如图,已知三棱柱 ,平面
,平面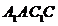 ⊥平面
⊥平面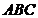 ,
,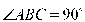 ,
,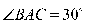 ,
,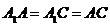 ,E,F分别是AC,
,E,F分别是AC, 的中点.
的中点.
(1)证明: 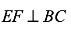
(2)求直线EF与平面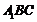 所成角的余弦值
所成角的余弦值
20.设等差数列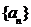 的前n项和为
的前n项和为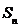 ,
,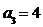 ,
,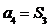 ,数列
,数列 满足:对每个
满足:对每个 ,
,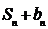 ,
,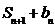 ,
,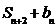 成等比数列.
成等比数列.
(1)求数列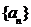 ,
,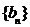 的通项公式
的通项公式
(2)记 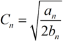 ,
, ,证明:
,证明: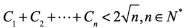 ABC-A柱子﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX﷽﷽﷽﷽﷽XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
ABC-A柱子﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽﷽XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX﷽﷽﷽﷽﷽XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
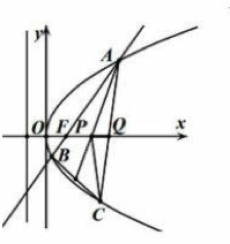
21.(本题满分15分)过焦点F(1,0)的直线与抛物线 交于A,B 两点,C 在抛物线,
交于A,B 两点,C 在抛物线,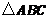 的重心P在x轴上,AC交x轴于点Q(点Q在点P的右侧)。
的重心P在x轴上,AC交x轴于点Q(点Q在点P的右侧)。
(1)求抛物线方程及准线方程;
(2)记 ,
,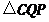 的面积分别为
的面积分别为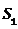 ,
,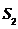 ,求
,求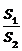 的最小值及此时点P的坐标。
的最小值及此时点P的坐标。
22.已知实数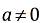 ,设函数
,设函数
(1)当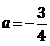 时,求函数
时,求函数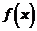 的单调区间
的单调区间
(2)对任意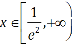 均有
均有  ,求
,求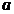 的取值范围
的取值范围