专题:
圆的一般方程是x²+y²+Dx+Ey+F=0(D²+E²-4F>0),其中圆心坐标是(-D/2,-E/2)。半径:1/2√(D²+E²-4F)。

圆的一般方程
圆的一般方程,是数学领域的知识。圆的一般方程为x²+y²+Dx+Ey+F=0(D²+E²-4F>0),或可以表示为(X+D/2)²+(Y+E/2)²=(D²+E²-4F)/4。
标准方程:圆半径的长度定出圆周的大小,圆心的位置确定圆在平面上的位置。如果已知:(1)圆半径长R;(2)中心A的坐标(a,b),则圆的大小及其在平面上关于坐标轴的位置就已确定(如下图)。根据图形的几何尺寸与坐标的联系可以得出圆的标准方程。结论如下:(x-a)²+(y-b)²=R²。
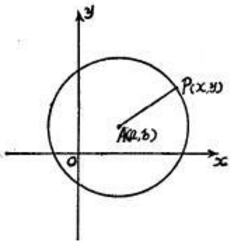
当圆的中心A与原点重合时,即原点为中心时,即a=b=0,圆的方程为:x²+y²=R²。
圆的定义
在同一平面内到定点的距离等于定长的点的集合叫做圆。这个定点叫做圆的圆心。
圆形一周的长度,就是圆的周长。能够重合的两个圆叫等圆,等圆有无数条对称轴。
圆是一个正n边形(n为无限大的正整数),边长无限接近0但永远无法等于0。