专题:
平行四边形对角线定理:2a²+2b²=c²+d²。其中c、d分别为平行四边形两条对角线长度,a、b分别为平行四边形两条邻边长度。

平行四边形平方和定理
平行四边形的四条边的边长的平方和等于对角线长的平方和。
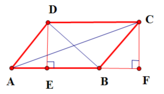
设平行四边形ABCD,作DE⊥AB于E,CF⊥AB,交AB延长线于F。
∵四边形ABCD是平行四边形
∴AB//DC,AB=DC,AD=BC
∴DE=CF(平行线间的距离相等)
∴Rt△ADE≌Rt△BCF(HL)(两个直角三角形完全相同)
∴AE=BF
根据勾股定理
AC²=AF²+CF²=(AB+BF)²+CF²
BD²=BE²+DE²=(AB-AE)²+DE²=(AB-BF)²+CF²
AC²+BD²=(AB+BF)²+CF²+(AB-BF)²+CF²
=(AB²+2AB*BF+BF²)+CF²+(AB²-2AB*BF+BF²)+CF²=2AB²+2BF²+2CF²
∵BF²+CF²=BC²(勾股定理)
∴AC²+BD²=2AB²+2BC²=AB²+CD²+BC²+AD²
平行四边形对角线性质
如果一个四边形是平行四边形,那么这个四边形的两条对角线互相平分。
过平行四边形对角线交点的直线,将平行四边形分成全等的两部分图形。
平行四边形是中心对称图形,对称中心是两对角线的交点。
平行四边形ABCD中,AC、BD是平行四边形ABCD的对角线,则各四边的平方和等于对角线的平方和。
平行四边形对角线把平行四边形面积分成四等份。