专题:
数列极限定义证明步骤证明:对任意的ε>0,解不等式│1/√n│=1/√n<ε,得n>1/ε²,取N=[1/ε²]+1...

证明步骤
证明:对任意的ε>0,解不等式
│1/√n│=1/√n<ε
得n>1/ε²,取N=[1/ε²]+1。
于是,对任意的ε>0,总存在自然数取N=[1/ε²]+1。
当n>N时,有│1/√n│<ε
故lim(n->∞)(1/√n)=0。
数列极限
数列的极限问题是我们学习的一个比较重要的部分,同时,极限的理论也是高等数学的基础之一。数列极限的问题作为微积分的基础概念,其建立与产生对微积分的理论有着重要的意义。
数列极限定义
定义设为数列{an},a为定数。若对任给的正数ε,总存在正整数N,使得当n>N时有
▏an-a▕<E则称数列{an}收敛于a,定数a称为数列{an}的极限,并记作
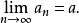
若数列{an}没有极限,则称{an}不收敛,或称{an}发散。
等价定义任给ε>0,若在(a-ε,a+ε)之外数列{an}中的项至多只有有限个,则称数列{an}收敛于极限a。