专题:
inx的导数等于y'= 1/x。inx求导:y=(lnx)‘=1/x,f(x)=logaX f(x)=1/xlna (a>0且a不等于1,x>0),f(x)=lnx f(x)=1/x (x>0)。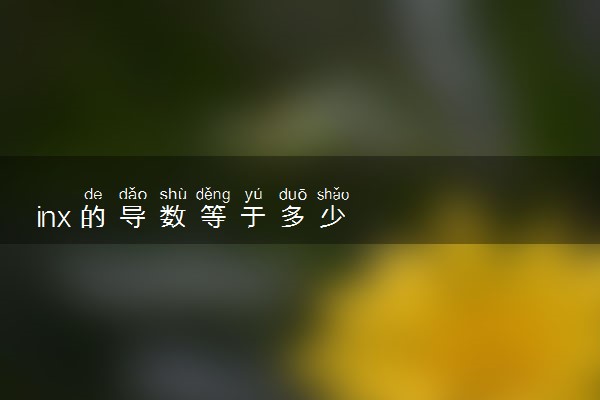
inx的导数怎样算的
具体过程如下:
(lnx)'=lim(dx->0) ln(x+dx) -lnx / dx
=lim(dx->0) ln(1+dx /x) / dx
dx/x趋于0,那么ln(1+dx /x)等价于dx /x
所以lim(dx->0) ln(1+dx /x) / dx
=lim(dx->0) (dx /x) / dx
=1/x
即y=lnx的导数是y'= 1/x
inx的导数定义
如果函数f(x)在(a,b)中每一点处都可导,则称f(x)在(a,b)上可导,则可建立f(x)的导函数,简称导数,记为f'(x)。
如果f(x)在(a,b)内可导,且在区间端点a处的右导数和端点b处的左导数都存在,则称f(x)在闭区间[a,b]上可导,f'(x)为区间[a,b]上的导函数,简称导数。
若将一点扩展成函数f(x)在其定义域包含的某开区间I内每一个点,那么函数f(x)在开区间内可导,这时对于内每一个确定的值,都对应着f(x)的一个确定的导数,如此一来每一个导数就构成了一个新的函数,这个函数称作原函数f(x)的导函数,记作:y'或者f′(x)。