专题:
射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。

影射定理
影射定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。射影定理是数学图形计算的重要定理。
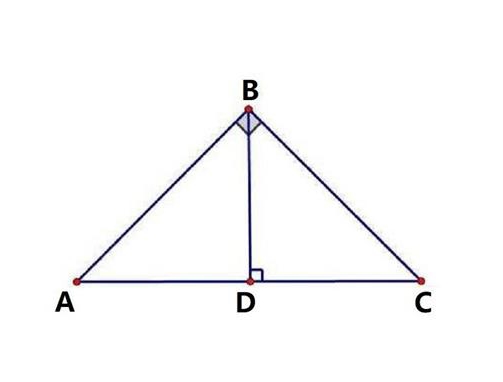
在Rt△ABC中,∠ABC=90°,BD是斜边AC上的高,则有射影定理如下:
BD²=AD·CD
AB²=AC·AD
BC²=CD·AC
由古希腊著名数学家、《几何原本》作者欧几里得提出。
验证推导
证明:①∵CD²+AD²=AC²,CD²+BD²=BC²
∴2CD²+AD²+BD²=AC²+BC²
∴2CD²=AB²-AD²-BD²
∴2CD²=(AD+BD)²-AD²-BD²
∴2CD²=AD²+2AD·BD+BD²-AD²-BD²
∴2CD²=2AD·BD
∴CD²=AD·BD