专题:
标准型的一元三次方程ax³+bx²+cx+d=0(a,b,c,d∈R,且a≠0),其解法有:1、意大利学者卡尔丹于1545年发表的卡尔丹公式法;2、中国学者范盛金于1989年发表的盛金公式法。
一元三次方程通用求根公式
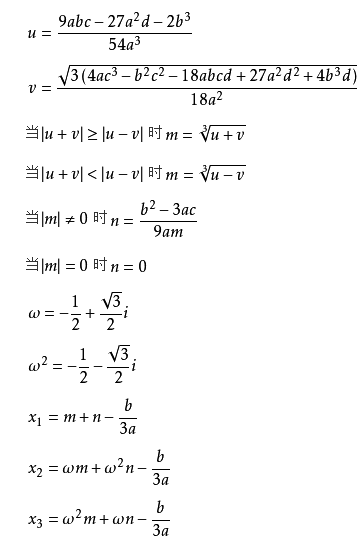
一元三次方程的因式分解法
例题:x³-3x²+4
答案:x1=-1,x2=x3=2
解题思路:解一元三次方程,首先要得到一个解,这个解可以凭借经验或者凑数得到,然后根据短除法得到剩下的项。
具体过程:我们观察式子,很容易找到x=-1是方程的一个解,所以我们就得到一个项x+1。
剩下的项我们用短除法。也就是用x³-3x²+4除以x+1。
因为被除的式子最高次数是3次,所以一定有x²
现在被除的式子变成了x³-3x²+4-(x+1)*x²=-4x²+4,因为最高次数项是-4x²,所以一定有-4x
现在被除的式子变成了-4x²+4-(-4x²-4x)=4x+4,剩下的一项自然就是4了
所以,原式可以分解成(x+1)*(x²-4x+4),也就是(x+1)*(x-2)²
(x+1)*(x-2)²=0
解得x1=-1,x2=x3=2