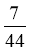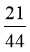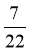台山一中2024届高三第一次月考数学试题
台山一中2024届高三第一次月考数学试题
2023-08
一、单选题(本大题共8小题,共40分.在每小题列出的选项中,选出符合题目的一项)
1. 设集合 ,
,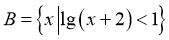 ,则
,则 ( )
( )
A. 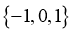 B.
B. 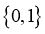 C.
C. 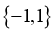 D.
D. 
【答案】B
【解析】
【分析】求出集合 、
、 ,利用交集的定义可求得集合
,利用交集的定义可求得集合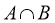 .
.
【详解】因为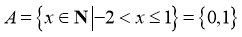 ,
,
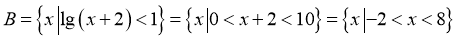 ,
,
所以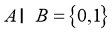 .
.
故选:B.
2. 已知i为虚数单位,若复数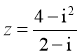 ,则
,则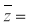 ( )
( )
A.  B.
B.  C.
C.  D.
D. 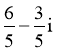
【答案】B
【解析】
【分析】由复数的运算化简复数 ,再求共轭复数即可.
,再求共轭复数即可.
【详解】因为 ,所以
,所以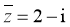 .
.
故选:B.
3. “ ”是“方程
”是“方程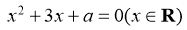 有正实数根”的( )
有正实数根”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】B
【解析】
【分析】根据零点 几何意义,将方程有正根问题等价转化为函数求零点问题,结合二次函数的性质,可得答案.
几何意义,将方程有正根问题等价转化为函数求零点问题,结合二次函数的性质,可得答案.
【详解】由方程 有正实数根,则等价于函数
有正实数根,则等价于函数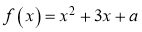 有正零点,
有正零点,
由二次函数 的对称轴为
的对称轴为 ,则函数
,则函数 只能存在一正一负的两个零点,
只能存在一正一负的两个零点,
则 ,解得
,解得 ,
,
故选:B.
4. 已知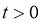 ,则函数
,则函数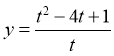 的最小值为
的最小值为
A.  B.
B.  C. 1 D. 2
C. 1 D. 2
【答案】A
【解析】
【分析】先分离,再根据基本不等式求最值,即得结果.
【详解】 ,当且仅当
,当且仅当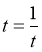 ,即
,即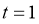 时,等号成立.
时,等号成立.
选A
【点睛】本题考查利用基本不等式求最值,考查基本分析求解能力,属基础题.
5.  展开式中含
展开式中含 的系数是( )
的系数是( )
A. 28 B. 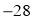 C. 84 D.
C. 84 D. 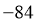
【答案】C
【解析】
【分析】根据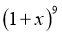 展开式的通项,分别求出展开式中含
展开式的通项,分别求出展开式中含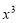 、
、 、
、 的项的系数,即可得出答案.
的项的系数,即可得出答案.
【详解】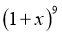 展开式的通项为
展开式的通项为 ,
, .
.
当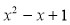 选取
选取 时,由已知可得,应选取
时,由已知可得,应选取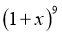 展开式中含
展开式中含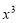 的项,
的项,
由 ,可得
,可得 ;
;
当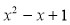 选取
选取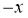 时,由已知可得,应选取
时,由已知可得,应选取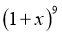 展开式中含
展开式中含 的项,
的项,
由 ,可得
,可得 ;
;
当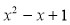 选取
选取 时,由已知可得,应选取
时,由已知可得,应选取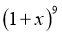 展开式中含
展开式中含 的项,
的项,
由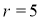 ,可得
,可得 .
.
所以, 展开式中含
展开式中含 的系数是
的系数是 .
.
故选:C.
6. 2023年武汉马拉松于4月16日举行,组委会决定派小王、小李等6名志愿者到甲乙两个路口做引导员,每位志愿者去一个路口,每个路口至少有两位引导员,若小王和小李不能去同一路口,则不同的安排方案种数为( )
A. 40 B. 28 C. 20 D. 14
【答案】B
【解析】
【分析】根据题意,先分配特殊的两个人,再将剩余4个人分到两个路口,按照分组分配相关知识进行计算即可.
【详解】若小王在1号路口,小李在2号路口,则剩余4个人分到两个路口,
两个路口为 人分布,共有
人分布,共有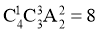 种方案,
种方案,
两个路口为 人分布,共有
人分布,共有 种方案,
种方案,
此时共有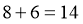 种方案;
种方案;
同理若小王在2号路口,小李在1号路口,也共有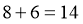 种方案.
种方案.
所以一共有28种不同的安排方案种数.
故选:B
7. 设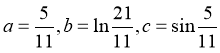 ,则( )
,则( )
A. 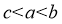 B.
B. 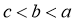 C.
C. 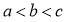 D.
D. 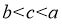
【答案】A
【解析】
【分析】构造函数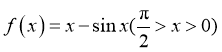 和
和 ,利用导数求解单调性,即可判断.
,利用导数求解单调性,即可判断.
【详解】当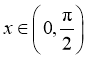 时,记
时,记 ,则
,则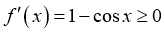 ,故
,故 在
在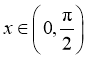 单调递增,故
单调递增,故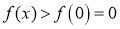 ,因此得当
,因此得当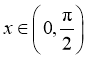 时,
时,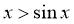 ,故
,故 ,即
,即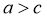 ;
;
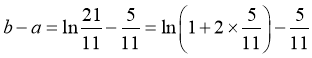 ,设
,设 ,则
,则 ,因为
,因为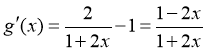 ,
,
当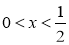 时,
时, .所以
.所以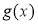 在
在 上单调递增,所以
上单调递增,所以 ,即
,即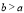 ,所以
,所以 .
.
故选:A
8. 设函数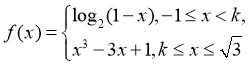 的值域为A,若
的值域为A,若 ,则
,则 的零点个数最多是( )
的零点个数最多是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
【分析】分别求出各段函数的单调性,结合函数图象分类讨论,分别求出函数的零点个数,即可判断;
【详解】解:令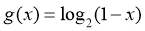 ,则
,则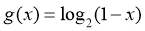 在
在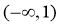 上单调递减;
上单调递减;
令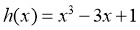 ,则
,则 .由
.由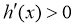 ,得
,得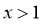 或
或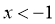 ;
;
由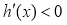 ,得
,得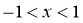 ,所以
,所以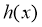 在
在 和
和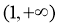 上单调递增,在
上单调递增,在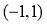 上单调递减,
上单调递减,
于是,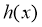 的极大值为
的极大值为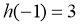 ,极小值为
,极小值为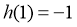 .在同一坐标系中作出函数
.在同一坐标系中作出函数 和
和 的图象,如下图:
的图象,如下图:
显然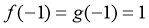 ;由
;由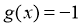 ,得
,得 ;由
;由 的解析式,得
的解析式,得 .
.
(1)若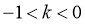 ,当
,当 时,
时,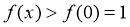 ,不符合题意;
,不符合题意;
(2)若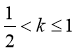 ,当
,当 时,
时, ,不符合题意;
,不符合题意;
(3)若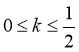 ,
,
①当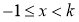 时,
时,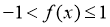 ;
;
②当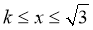 时,
时,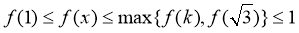 ,即
,即 .
.
由①②,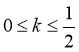 时符合题意.
时符合题意.
此时,结合图象可知,当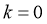 时,
时, 在
在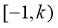 上没有零点,在
上没有零点,在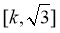 上有2个零点;
上有2个零点;
当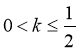 时,
时, 在
在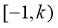 上有1个零点,在
上有1个零点,在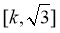 上有1个或2个零点,
上有1个或2个零点,
综上, 最多有3个零点.
最多有3个零点.
故选:C.
二、多选题(本大题共4小题,共20分.在每小题有多项符合题目要求)
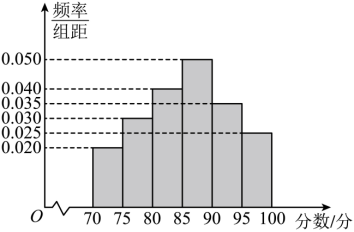
9. 《国家学生体质健康标准》是国家学校教育工作的基础性指导文件和教育质量基本标准,它适用于全日制普通小学、初中、普通高中、中等职业学校、普通高等学校的学生.某高校组织 名大一新生进行体质健康测试,现抽查200名大一新生的体测成绩,得到如图所示的频率分布直方图,其中分组区间为
名大一新生进行体质健康测试,现抽查200名大一新生的体测成绩,得到如图所示的频率分布直方图,其中分组区间为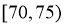 ,
,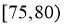 ,
, ,
, ,
, ,
,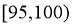 .则下列说法正确的是( )
.则下列说法正确的是( )
A. 估计该样本的众数是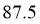
B. 估计该样本的均值是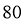
C. 估计该样本的中位数是
D. 若测试成绩达到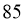 分方可参加评奖,则有资格参加评奖的大一新生约为
分方可参加评奖,则有资格参加评奖的大一新生约为 人
人
【答案】ACD
【解析】
【分析】根据频率分布直方图,可判断A项;根据频率分布直方图,估计出平均数,可判断B项;根据频率分布直方图,估计出中位数,可判断C项;根据频率分布直方图,测试成绩达到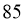 分的频率为
分的频率为 ,即可估算有资格参加评奖的人数.
,即可估算有资格参加评奖的人数.
【详解】对于A项,由频率分布直方图可得,最高小矩形为 ,所以可估计该样本的众数是
,所以可估计该样本的众数是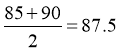 ,故A项正确;
,故A项正确;
对于B项,由频率分布直方图,可估计该样本的均值是
 ,故B项错误;
,故B项错误;
对于C项,由频率分布直方图可得,成绩在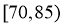 之间的频率为
之间的频率为 ,
,
在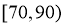 之间的频率为
之间的频率为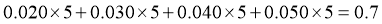 ,
,
所以可估计该样本的中位数在 内.
内.
设中位数为 ,则由
,则由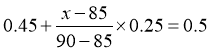 可得,
可得, ,故C项正确;
,故C项正确;
对于D项,由频率分布直方图可得,测试成绩达到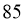 分的频率为
分的频率为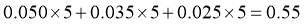 ,所以可估计有资格参加评奖的大一新生约为
,所以可估计有资格参加评奖的大一新生约为 人,故D项正确.
人,故D项正确.
故选:ACD.
10. 已知非零实数a,b满足 ,则下列不等关系一定成立的是( )
,则下列不等关系一定成立的是( )
A. 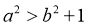 B.
B. 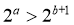
C. 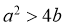 D.
D. 
【答案】ABC
【解析】
【分析】利用不等式的性质及特殊值法判断即可.
【详解】解:对于非零实数 ,
,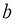 满足
满足 ,则
,则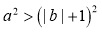 ,
,
即 ,故A一定成立;
,故A一定成立;
因为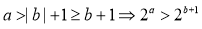 ,故B一定成立;
,故B一定成立;
又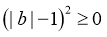 ,即
,即 ,所以
,所以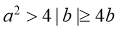 ,故C一定成立;
,故C一定成立;
对于D:令 ,
, ,满足
,满足 ,此时
,此时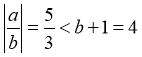 ,故D不一定成立.
,故D不一定成立.
故选:ABC
11. 下列关于概率统计说法中正确的是 ( )
( )
A. 两个变量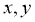 的相关系数为
的相关系数为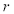 ,则
,则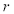 越小,
越小, 与
与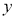 之间的相关性越弱
之间的相关性越弱
B. 设随机变量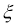 服从正态分布
服从正态分布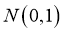 ,若
,若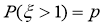 ,则
,则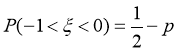
C. 在回归分析中,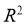 为
为 的模型比
的模型比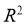 为
为 的模型拟合的更好
的模型拟合的更好
D. 某人在 次答题中,答对题数为
次答题中,答对题数为 ,
,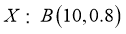 ,则答对
,则答对 题的概率最大
题的概率最大
【答案】BCD
【解析】
【分析】由相关系数,正态分布,二项分布的概念判断.
【详解】对于A,两个变量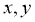 的相关系数为
的相关系数为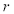 ,
, 越小,
越小, 与
与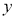 之间的相关性越弱,故A错误,
之间的相关性越弱,故A错误,
对于B,随机变量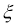 服从正态分布
服从正态分布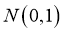 ,由正态分布概念知若
,由正态分布概念知若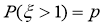 ,则
,则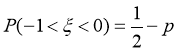 ,故B正确,
,故B正确,
对于C,在回归分析中,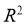 越接近于
越接近于 ,模型的拟合效果越好,所以
,模型的拟合效果越好,所以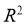 为
为 的模型比
的模型比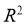 为
为 的模型拟合的更好,故C正确,
的模型拟合的更好,故C正确,
对于D,某人在 次答题中,答对题数为
次答题中,答对题数为 ,
,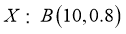 ,则数学期望
,则数学期望 ,说明答对
,说明答对 题的概率最大,故D正确.
题的概率最大,故D正确.
故选:BCD
12. 已知函数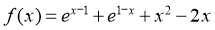 ,若不等式
,若不等式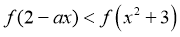 对任意
对任意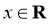 恒成立,则实数
恒成立,则实数 的取值可能是( )
的取值可能是( )
A. 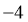 B.
B. 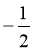 C.
C.  D.
D. 
【答案】BC
【解析】
【分析】令 ,得到
,得到 ,推得
,推得 为偶函数,得到
为偶函数,得到 的图象关于
的图象关于 对称,再利用导数求得当
对称,再利用导数求得当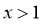 时,
时, 单调递增,当
单调递增,当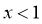 时,
时, 单调递减,把不等式转化为
单调递减,把不等式转化为 恒成立,结合二次函数的性质,即可求解.
恒成立,结合二次函数的性质,即可求解.
【详解】由函数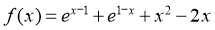 ,
,
令 ,则
,则 ,可得
,可得 ,
,
可得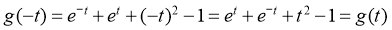 ,
,
所以 为偶函数,即函数
为偶函数,即函数 的图象关于
的图象关于 对称,
对称,
又由 ,令
,令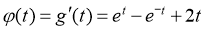 ,
,
可得 ,所以
,所以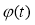 为单调递增函数,且
为单调递增函数,且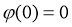 ,
,
当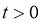 时,
时,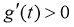 ,
, 单调递增,即
单调递增,即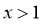 时,
时, 单调递增;
单调递增;
当 时,
时, ,
, 单调递减,即
单调递减,即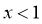 时,
时, 单调递减,
单调递减,
由不等式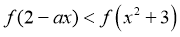 ,可得
,可得 ,即
,即
所以不等式 恒成立,即
恒成立,即 恒成立,
恒成立,
所以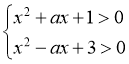 的解集为
的解集为 ,所以
,所以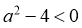 且
且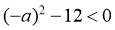 ,
,
解得 ,结合选项,可得BC适合.
,结合选项,可得BC适合.
故选:BC.
【点睛】关键点睛:本题 关键是利用换元法设
关键是利用换元法设 ,从而得到
,从而得到 ,证明其为偶函数,则得到
,证明其为偶函数,则得到 的图象关于
的图象关于 对称,再结合其单调性即可得到不等式组,解出即可.
对称,再结合其单调性即可得到不等式组,解出即可.
三、填空题(本大题共4小题,共20分)
13. 若命题“ ”是假命题,则实数
”是假命题,则实数 的最大值为______.
的最大值为______.
【答案】
【解析】
【分析】由命题的否定转化为恒成立问题,利用二次函数的性质即可求解.
【详解】由题知命题的否定“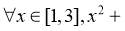
 ”是真命题.令
”是真命题.令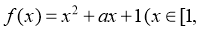
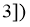 ,则
,则 解得
解得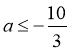 ,故实数
,故实数 的最大值为
的最大值为
故答案为:
14. 已知向量 满足
满足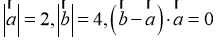 ,则
,则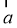 与
与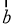 的夹角为___________.
的夹角为___________.
【答案】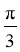
【解析】
【分析】根据平面向量数量积的运算性质,结合平面向量夹角公式进行求解即可.
【详解】由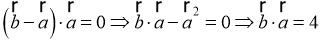 ,
,
 ,
,
故答案为: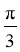
15. 已知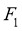 ,
,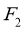 为椭圆C的两个焦点,P为C上一点,若
为椭圆C的两个焦点,P为C上一点,若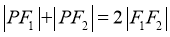 ,则C的离心率为______.
,则C的离心率为______.
【答案】 .
.
【解析】
【分析】利用椭圆的定义及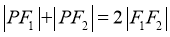 ,得到
,得到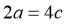 ,进而得解.
,进而得解.
【详解】 为椭圆
为椭圆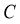 上一点,由椭圆的定义知,
上一点,由椭圆的定义知,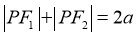 ,
,
因为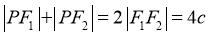 ,
,
所以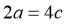 ,所以
,所以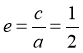 .
.
故答案为: .
.
【点睛】本题考查椭圆的离心率的求解及椭圆的定义,属于基础题.
16. 某校决定从高一、高二两个年级分别抽取100人、60人参加演出活动,高一100人中女生占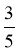 ,高二60人中女生占
,高二60人中女生占 ,则从中抽取1人恰好是女生的概率为______.
,则从中抽取1人恰好是女生的概率为______.
【答案】
【解析】
【分析】根据条件概率公式即可求解.
【详解】用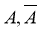 分别表示取的一人是来自高一和高二,
分别表示取的一人是来自高一和高二, 表示抽取一个恰好是女生,则由已知可知:
表示抽取一个恰好是女生,则由已知可知: ,且
,且 ,
,
所以
故答案为:
四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17. 在 中,
中,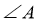 =60°,c=
=60°,c=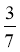 a.
a.
(1)求sinC的值;
(2)若a=7,求 的面积.
的面积.
【答案】(1)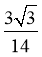
(2)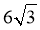
【解析】
【分析】(1)直接利用正弦定理求解即可,
(2)求出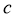 ,再利用余弦定理求出
,再利用余弦定理求出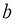 ,然后利用三角形面积公式可求得答案
,然后利用三角形面积公式可求得答案
【小问1详解】
在 中,因为
中,因为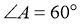 ,
,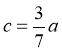 ,
,
所以由正弦定理得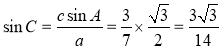 .
.
【小问2详解】
因为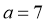 ,所以
,所以 .
.
由余弦定理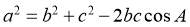 得
得 ,
,
解得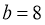 或
或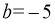 (舍).
(舍).
所以 的面积
的面积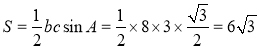 .
.
18. 设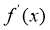 为函数
为函数 的导函数,已知
的导函数,已知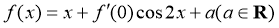 ,且
,且 的图像经过点
的图像经过点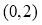 .
.
(1)求曲线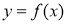 在点
在点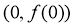 处的切线方程;
处的切线方程;
(2)求函数 在
在 上的单调区间.
上的单调区间.
【答案】(1)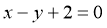
(2)单调递增区间为 和
和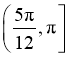 ;单调递减区间为
;单调递减区间为
【解析】
 分析】(1)求导,计算
分析】(1)求导,计算 得到切线斜率,点斜式求切线方程.
得到切线斜率,点斜式求切线方程.
(2)求出函数解析式,求导函数,由导函数的正负解得原函数的单调区间.
【小问1详解】
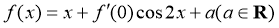 ,则
,则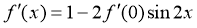 ,得
,得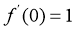 .
.
由题意 ,可得曲线
,可得曲线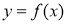 在点
在点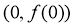 处的切线方程为
处的切线方程为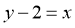 ,即
,即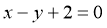 .
.
【小问2详解】
由已知得 .
.
又由(1)知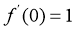 ,所以
,所以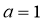 .
.
故 .
.
 ,
,
由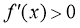 ,得
,得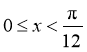 ,或
,或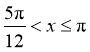 ;由
;由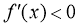 ,得
,得 .
.
故 在
在 上的单调递增区间为
上的单调递增区间为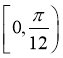 和
和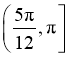 ;单调递减区间为
;单调递减区间为 .
.
19. 已知图1是由等腰直角三角形 和菱形
和菱形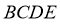 组成的一个平面图形,其中菱形边长为4,
组成的一个平面图形,其中菱形边长为4, ,
, .将三角形
.将三角形 沿
沿 折起,使得平面
折起,使得平面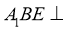 平面
平面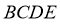 (如图2).
(如图2).

(1)求证: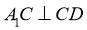 ;
;
(2)求二面角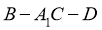 的正弦值.
的正弦值.
【答案】(1)证明见解析
(2)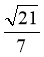
【解析】
【分析】(1)取 的中点
的中点 ,连接
,连接 ,
, ,则
,则 ,再结合已知面面垂直可得
,再结合已知面面垂直可得 平面
平面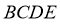 ,则
,则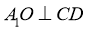 ,而
,而 ,再由线面垂直的判定可得
,再由线面垂直的判定可得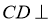 面
面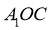 ,从而可证得
,从而可证得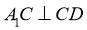 ,
,
(2)以 ,
,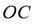 ,
, 所在的直线分别为
所在的直线分别为 轴,
轴,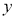 轴,
轴, 轴建立空间直角坐标系,利用空间向量求解.
轴建立空间直角坐标系,利用空间向量求解.
【小问1详解】
证明:取 的中点
的中点 ,连接
,连接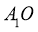 ,
,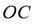 .
.
∵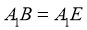 ,∴
,∴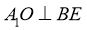 .
.
又∵平面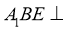 平面
平面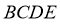 ,且平面
,且平面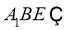 平面
平面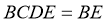 ,
, 平面
平面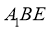 ,
,
∴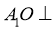 平面
平面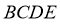 .
.
∵ 平面
平面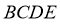 ,∴
,∴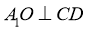 .
.
∵在菱形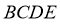 中,
中, , ∴
, ∴ 为等边三角形,
为等边三角形,
∵ 的中点为
的中点为 ,∴
,∴ ,
,
∵ ∥
∥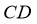 ,∴
,∴
∵ ,
,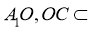 平面
平面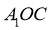 ,
,
∴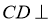 平面
平面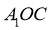 ,∵
,∵ 平面
平面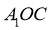 ,∴
,∴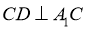 .
.
【小问2详解】
由(1)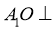 平面
平面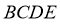 ,∵
,∵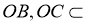 平面
平面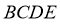 ,∴
,∴ ,
,
∵ ,
,
∴如图,以 ,
, ,
, 所在的直线分别为
所在的直线分别为 轴,
轴, 轴,
轴, 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则
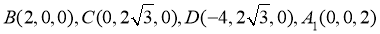 ,
,
∴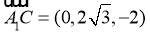 ,
, ,
,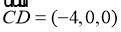 .
.
设平面 的法向量为
的法向量为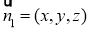 ,则
,则
 ,不妨设
,不妨设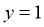 ,则
,则 .
.
设平面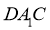 的法向量为
的法向量为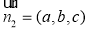 ,则
,则
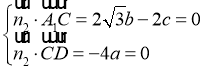 ,令
,令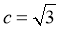 ,则
,则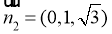 ,
,
设二面角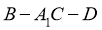 的大小为
的大小为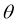 ,由图可知
,由图可知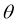 为钝角,
为钝角,
∴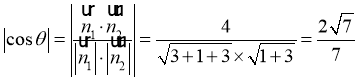 ,∴
,∴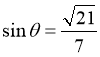 .
.
∴二面角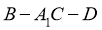 的正弦值为
的正弦值为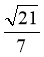 .
.
20. 已知数列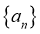 的首项
的首项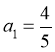 ,且满足
,且满足 ,设
,设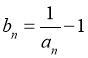 .
.
(1)求证:数列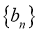 为等比数列;
为等比数列;
(2)若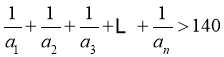 ,求满足条件的最小正整数
,求满足条件的最小正整数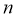 .
.
【答案】(1)证明见解析
(2)140
【解析】
【分析】(1)利用等比数列的定义证明即可;
(2)利用分组求和的方法得到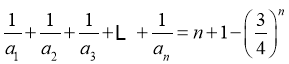 ,然后利用
,然后利用 的增减性解不等式
的增减性解不等式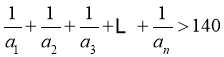 即可.
即可.
【小问1详解】
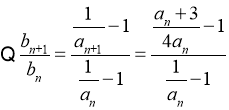
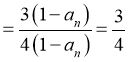 ,
,
 ,所以数列
,所以数列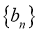 为首项为
为首项为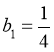 ,公比为
,公比为 等比数列.
等比数列.
【小问2详解】
由(1)可得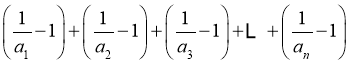

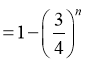 ,
,
即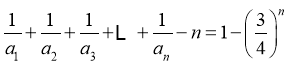
∴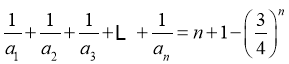
而 随着
随着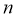 的增大而增大
的增大而增大
要使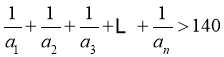 ,即
,即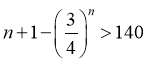 ,则
,则 ,
,
∴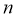 的最小值为140.
的最小值为140.
21. 已知椭圆E: 与y轴的正半轴相交于点M,点F1,F2为椭圆的焦点,且
与y轴的正半轴相交于点M,点F1,F2为椭圆的焦点,且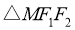 是边长为2的等边三角形,若直线l:y=kx+2
是边长为2的等边三角形,若直线l:y=kx+2 与椭圆E交于不同的两点A,B.
与椭圆E交于不同的两点A,B.
(1)直线MA,MB的斜率之积是否为定值?若是,请求出该定值,若不是,请说明理由;
(2)求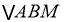 的面积的最大值.
的面积的最大值.
【答案】(1)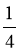 ;(2)
;(2)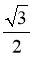 .
.
【解析】
【详解】(1)因为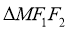 是边长为2的等边三角形,
是边长为2的等边三角形,
所以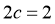 ,
,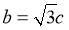 ,
, ,所以
,所以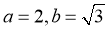 ,
,
所以椭圆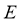 :
: ,点
,点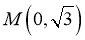 .
.
将直线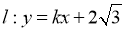 代入椭圆
代入椭圆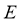 的方程,
的方程,
整理得: ,(*)
,(*)
设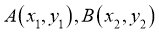 ,则由(*)式可得
,则由(*)式可得
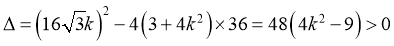 ,
,
所以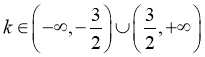 ,
,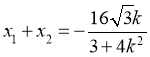 ,
, ,
,
所以直线 的斜率之积
的斜率之积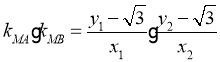
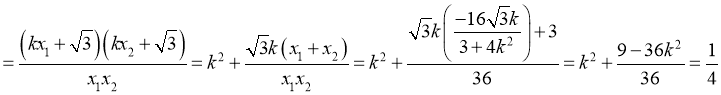
所以直线
 斜率之积是定值
斜率之积是定值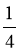 .
.
(2)记直线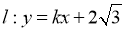 与
与 轴的交点为
轴的交点为 ,
,
则
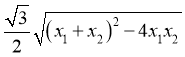

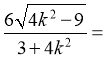
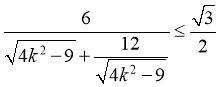
当且仅当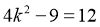 ,即
,即 时等号成立.
时等号成立.
所以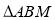 的面积的最大值为
的面积的最大值为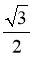 .
.
22. “英才计划”最早开始于2013年,由中国科协、教育部共同组织实施,到2022年已经培养了6000多名具有创新潜质的优秀中学生,为选拔培养对象,某高校在暑假期间从武汉市的中学里挑选优秀学生参加数学、物理、化学、信息技术学科夏令营活动.
(1)若化学组的12名学员中恰有5人来自同一中学,从这12名学员中选取3人,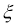 表示选取的人中来自该中学的人数,求
表示选取的人中来自该中学的人数,求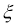 的分布列和数学期望;
的分布列和数学期望;
(2)在夏令营开幕式的晚会上,物理组举行了一次学科知识竞答活动.规则如下:两人一组,每一轮竞答中,每人分别答两题,若小组答对题数不小于3,则取得本轮胜利,假设每轮答题结果互不影响.已知甲、乙两位同学组成一组,甲、乙答对每道题的概率分别为 ,
,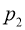 ,且
,且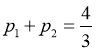 ,如果甲、乙两位同学想在此次答题活动中取得6轮胜利,那么理论上至少要参加多少轮竞赛?
,如果甲、乙两位同学想在此次答题活动中取得6轮胜利,那么理论上至少要参加多少轮竞赛?
【答案】(1)分布列见解析,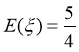
(2)11轮
【解析】
【分析】(1)根据超几何分布列分布列计算数学期望即可;
(2)先求每轮答题中取得胜利的概率的最大值,再应用独立重复实验数学期望的范围求出最少轮数.
【小问1详解】
由题意可知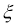 的可能取值有0、1、2、3,
的可能取值有0、1、2、3,
 ,
, ,
,
 ,
,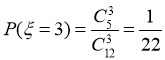
所以,随机变量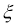 的分布列如下表所示:
的分布列如下表所示:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以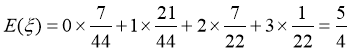 .
.
【小问2详解】
他们在每轮答题中取得胜利的概率为
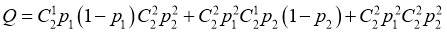
 ,
,
由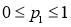 ,
, ,
,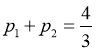 ,得
,得 ,
,
则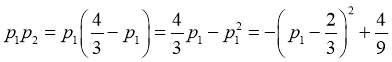 ,因此
,因此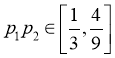 ,
,
令 ,
,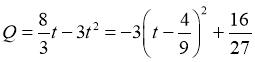 ,于是当
,于是当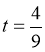 时,
时,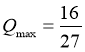 .
.
要使答题轮数取最小值,则每轮答题中取得胜利的概率取最大值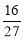 .
.
设他们小组在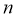 轮答题中取得胜利的次数为
轮答题中取得胜利的次数为 ,则
,则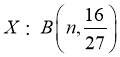 ,
,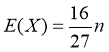 ,
,
由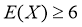 ,即
,即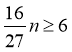 ,解得
,解得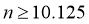 .
.
而 ,则
,则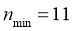 ,所以理论上至少要进行11轮答题.
,所以理论上至少要进行11轮答题.